皆さん、こんにちは。KOです。今回は乗算について説明していきます。乗算は簡単にいうと掛け算のことですが、検定ではパーセント(割合)の計算も必要となります。また、ラウンドセレクターや小数点セレクターを使う端数処理も出てくるので、少し難しいと感じるかもしれないですが、ここを理解してしまえば、第10回で説明する除算も基本的には同じなので非常に楽になります。今回は長いですが、途中で休憩をとりながらでも良いので、ぜひ頑張っていきましょう!ファイトです!
| 【今回の講座内容】 |
■乗算の概要
■端数処理の方法について
■無名数の計算(NO.1~NO.10)
■名数の計算(NO.11~NO.20)
■パーセントの計算
■採点と計算する順序について |
あと、ここでは聞きなれない単語がいくつか登場するので、予め簡単に説明しておきます♪
[無名数]単位のついていないただの数字 ※例)123
[名数]単位のついた数字 ※例)¥123
[端数処理]例えば小数点が出た時に四捨五入するのか、切り捨てるのかというような処理
[帯小数]1以上の小数 ※例)1.234
[小数]整数の部分が0の小数 ※例)0.123
■乗算の概要
乗算とは冒頭にも説明したように簡単にいうと、掛け算のことですが、検定では、無名数(NO.1~10)の計算、名数(NO.11~20)の計算、それぞれの小計、合計に対する個々の割合を求めるパーセントの計算があります。
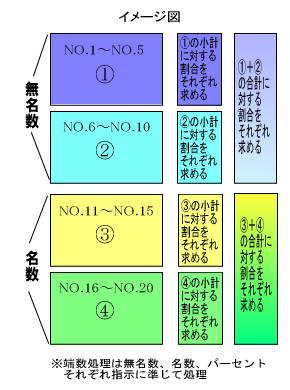
また、全ての計算において、端数処理が必要な場合は、ラウンドセレクター、小数点セレクターを用いながら計算していきます。この端数処理の方法については問題用紙の上に「(注意)」として、無名数、名数、パーセントそれぞれの処理方法が説明されていますので、それに準じて処理します。言葉だけでは分かりにくい部分もありますので、一応、左記にイメージ図を作りましたので重ねて参照下さい☆
あとは、レベルによって桁数が違ったり、パーセント以外の端数処理の問題数が異なります。当然ですが、上級になれば桁数も増えていきます。
ちなみにパーセント以外の端数処理については3級では2題(無名数1題、名数1題)、2級では4題(無名数2題、名数2題)、1級では8題(無名数4題、名数4題)出題されます。
乗算の概要は大体、こんなところです。
では、さっそく、全体のベースとなる端数処理の方法から説明していきたいと思います。 |
|
■端数処理の方法について
端数処理の方法については先程も触れましたが、問題の上に「(注意)」として記載されています。これは言い換えると、小数点セレクター、ラウンドセレクターをどう設定するかということになります。では、その「(注意)」の文を見てみましょう。
(注意)
無名数で小数第3位未満の端数が出たとき、名数で円位未満の端数が出たとき、パーセントの小数第2位未満の端数が出たときは四捨五入すること |
※全経の公式サイトの出題範囲より抜粋
初めて見る方は「ん?」となるかもしれませんが、3つの文に分けると理解しやすいと思います。
・無名数で小数第3位未満の端数が出たときは四捨五入すること
・名数で円位未満が出たときは四捨五入すること
・パーセントの小数第2位未満の端数が出たときは四捨五入すること
どうでしょうか。これだと分かりやすいですね^-^
では、実際に数字を当てはめながら、それぞれ説明していきたいと思います。
[無名数の場合(小数第3位未満の端数が出たときは四捨五入)・・・例 4.13758]
いきなり問題ですが4.13758の小数第3位未満はどこになるでしょうか? 小学生なら学校で慣れているので即答するかもしれないですが、小数に普段、関わりのない方であれば、おそらく年齢を重ねていくにつれ「あれ?小数の未満ってどうなんだっけ?」となってしまうのではないでしょうか?(笑)。答えは137までが小数第3位なので未満は58になります^-^
では、次にこの58の部分を四捨五入することとあるので四捨五入します。すると4.138になり、これが正解になります。今は暗算で四捨五入しましたが、これを電卓のセレクターの機能を使えば、自動で四捨五入してくれます。
まず、ラウンドセレクターを四捨五入を行う「5/4」に合わせます。次に小数点以下第3位まで表示させる必要があるので小数点セレクターを「3」に設定します。この状態で計算すれば、常に小数第3位未満は四捨五入して表示されます。もし、セレクターの使い方を忘れてしまった方は、第2回の電卓の機能を参照下さい。
[名数の場合(円位未満の端数が出たときは四捨五入)・・・例 ¥72.1]
続いて名数についてですが、円位未満が出たときは四捨五入とありますが、まず、円位未満とは何でしょうか? 円の最小の単位は1円なので、1円未満というのは小数のことになりますね。つまり、小数が出た場合は四捨五入するということなので、小数が答えになることはないことありません。例のケースだと¥72が正解になります。これを電卓で設定すると、小数は表示させないので小数点セレクターは「0」、ラウンドセレクターは「5/4」になります。
[パーセントの場合(小数第2位未満の端数が出たときは四捨五入)・・・例 53.7589%]
最後にパーセントについてですが、小数第2位未満を四捨五入とあるので、例の場合だと89の部分を四捨五入します。すると、53.76%となりますね。電卓のセレクターではラウンドセレクターを「5/4」、小数点セレクターを「2」に合わせて計算すればOKです。無名数の場合と小数の位が違うだけなので簡単ですね。
端数処理の方法については以上になりますが、よく分からなかったという方は、とりあえず「無名数の時はこれとこれ、名数の時はこれとこれを設定するんだな」と機械的に覚えてしまっても良いと思います☆
さて、次は無名数の計算、名数の計算、パーセントの計算について説明していきますが、初めての方は、ここから説明が長くなるので、この辺で一度休憩するとよいと思います♪
■無名数の計算(NO.1~NO.10)
無名数の計算はNO.1~NO.5(整数×整数)とNO.6~NO.10(小数or帯小数×小数or帯小数)の二つのグループに分かれています。また、グループごとに小計を計算し、最後は無名数としての合計を計算します。そして、これらの結果をもとに、後に説明するパーセントを計算していきます。
このように連係している為、1題でも計算ミスをしてしまうと、パーセントの計算に大きく響くので、確実に計算する事が重要になります。
あと、端数処理はどの級(レベル)でもNO.6~NO.10の中で発生するので、計算する直前にラウンドセレクターを「5/4」、小数点セレクターを「3」に設定してから計算しましょう。つまり、NO.1~NO.5では端数処理は発生しないということを抑えておきましょう
では、以上のことを踏まえ、下記の空欄になっている部分(※パーセントは除く)を計算してみましょう。また、小計や合計も忘れずに計算してみましょう。
【練習問題】(制限時間2分)
(注意)小数第3位未満の端数が出たときは四捨五入すること
| NO |
1 |
8,136×182 = 1,480,752 |
% |
% |
| 2 |
58,364×56 = 3,268,384 |
% |
% |
| 3 |
4,396×692 = |
% |
% |
| 4 |
9,056×263 = 2,381,728 |
% |
% |
| 5 |
7,686×758 = |
% |
% |
| NO.1~NO.5 小計① |
100 % |
| |
6 |
2.0625×1.68 = |
% |
% |
| 7 |
8.51×20.5 = 174.455 |
% |
% |
| 8 |
654.5×4.21 = 2,755.445 |
% |
% |
| 9 |
0.3748×0.713 = |
% |
% |
| 10 |
3.328×5.875 = |
% |
% |
| NO.6~NO.10 小計② |
100 % |
| (小計①+②) 合計 |
|
100 % |
※無名数の部分であるNO.1~NO.10のみを抜粋して載せています。
出来ましたでしょうか?まず、NO.1~5については、端数処理もなく、そのまま計算するだけなので簡単ですね。NO.3の答えは3,042,032、NO.5は5,825,988になります。
次にNO.6~NO.10ですが、この中に端数処理の問題が含まれています。実は全経の出題範囲の中にどの部分が端数処理になるのか記載があり、3級では小数×小数で1題出題されるとあるので、上記の問題であれば、NO.9が該当します。ただ、予めセレクターを設定して計算すると、端数が出ても常に小数第3位までしか表示されないので、端数処理の問題なのかは分かりません。従ってそこは気にせず計算するようにしましょう。ちなみに1級レベルになると5問中4問は端数処理になるので、気にするだけ時間の無駄になります。
さて、この問題の回答ですが、NO.6は3.465、NO.9は0.267、NO.10は19.552が答えなります。
あと小計、合計ですが、これはそのまま足すだけです。小計①はNO.1~5の結果を全て足して15,998,884となり、小計②はNO.6からNO.10の結果を全て足して2,953.184となります。合計は小計①+②なので16,001,837.184となります。
では、続いて名数の計算です。
■名数の計算(NO.11~NO.20)
名数の計算はNO.11~NO.15(名数×整数)とNO.16~NO.20(名数×小数or帯小数)の二つのグループに分かれています。また、グループごとに小計も計算し、最後は名数としての合計を計算します。そして、この結果をもとに、パーセントを計算していきます。
あと、端数処理はどの級(レベル)でもNO.16~NO.20の中で発生するので、計算する直前にラウンドセレクターを「5/4」、小数点セレクターを「0」に設定してから計算しましょう。つまり、NO.11~NO.15では端数処理は発生しないということを抑えておきましょう
読んで頂いても分かるように、基本的には無名数と似たような感じです。ただし、名数なので解答する際には¥が必要になります。
では下記の空欄になっている部分(※パーセントは除く)を計算してみましょう。また、小計や合計も忘れずに計算してみましょう。
【練習問題】(制限時間2分)
(注意)名数で円位未満が出たときは四捨五入すること
| NO |
11 |
¥5,286×675 = |
% |
% |
| 12 |
¥2,814×856 = ¥2,408,784 |
% |
% |
| 13 |
¥7,529×631 = |
% |
% |
| 14 |
¥38,541×29 = |
% |
% |
| 15 |
¥8,638×795 = ¥6,867,210 |
% |
% |
| NO.11~NO.15 小計③ |
100 % |
| |
16 |
¥8,775×3.32 = ¥29,133 |
% |
% |
| 17 |
¥2,520×0.625 = ¥1,575 |
% |
% |
| 18 |
¥7,562×15.5 = |
% |
% |
| 19 |
¥712×0.0567 = |
% |
% |
| 20 |
¥4,824×1.375 = |
% |
% |
| NO.16~NO.20 小計④ |
100 % |
| (小計③+④) 合計 |
|
100 % |
※名数の部分であるNO.11~NO.20のみを抜粋して載せています。
では解答です。まず、NO.11~NO.15についてはそのまま計算するだけですね。NO.11の答えは¥3,568,050、NO.13は¥4,750,799、NO.14は¥1,117,689になります。
次はNO.16~NO.20ですが、この中に端数処理の問題が含まれており、無名数同様に全経の出題範囲の中に端数処理について書かれていますが、気にせず計算しましょう。答えはNO.18が¥117,211、NO.19が¥40、NO.20が¥6,633になります。
あと小計、合計ですが、無名数の時と同様にそのまま足すだけです。小計③はNO.11~15の結果を足して¥18,712,532、小計④はNO.16からNO.20の結果を足して¥154,592となります。合計は小計③+④なので¥18,867,124となります。
さて、次はパーセントの計算です。
■パーセントの計算
いよいよ乗算の最後となるパーセントの計算ですが、解答欄を見て分かるようにパーセントの欄が2列あります。これは左側が小計①~④に対する個々の割合、右側が無名数、名数に対する個々の割合となっています。
また、ここでは、ほとんどの計算で端数処理が発生するので、予めセレクターを設定して計算していきます。もう、大丈夫だかと思いますが、小数第2位未満を四捨五入し、小数点以下第2位まで表示させる必要があるので、ラウンドセレクターを「5/4」、小数点セレクターは「2」に設定します。
ただ、パーセントの計算では解答する際に一つだけ注意しなければならない点があります。それは答えが0や9などのような整数の場合、もしくは1.1のように小数第1位で終わる場合でも、0.00、9.00、1.10のように、必ず小数第2位まで書かなければ不正解になりますので注意しましょう。
では、小計①に対するNO.1~NO.5の割合を例に挙げて左側の列パーセントから説明していきます
≪左側の列のパーセントについて≫
まず、割合を求める計算式ですが、これはスタンダードに割合=個÷全体×100になります。特に電卓検定だからと言って何かが違うといったことはありません。では実際にこの式を用いて当てはめながら見ていきましょう。
NO.1の場合だと個が1,480.752で、全体が小計①の15,998,884になるので、式は下記のようになります。
割合=1,480.752÷15,998,884×100
NO.1の答えは四捨五入されるので9.26になります。あとはNO.2~NO.5も同様に計算します。このことからも分かると思いますが、全体となる小計①はNO.2~NO.5でも使用するので、M+を押し、電卓に記憶させて、計算を繰り返すようにしましょう。
小計②に対するNO.6~NO.10も、同じように「割合=個(NO.6~NO.10)÷全体(小計②)×100」でそれぞれ計算しくていくだけになります。
ちなみに慣れてくると、最後に100を掛け算するのが面倒になり、あらかじめ、個を100倍した状態で計算することも出来るようになります。
【例】
NO.1の場合:割合=148,075,200÷小計①
NO.9の場合:2.67÷小計②
ただし、単純に100を掛けるだけとはいえ、計算ミスをする可能性もあるので、最初はスタンダードに計算した方がよいかもしれません。
≪右側の欄のパーセントについて≫
続いて右側の欄のパーセントについてですが、これも簡単です。ここでは小計①と小計②を足した無名数の合計に対してのNO.1~NO.10の割合を求める計算になりますので、式で表すと「割合=個(NO.1~NO.10)÷全体(合計)×100」になります。あとはNO.1~NO.10までそれぞれ、計算していくだけになります。
【練習問題】(制限時間2分)
では下記で空欄になっている名数のパーセントについて、それぞれ計算してみましょう。
(注意)パーセントの小数第2位未満の端数が出たときは四捨五入すること
| NO |
1 |
8,136×182 = 1,480,752 |
9.26 % |
9.25 % |
| 2 |
58,364×56 = 3,268,384 |
20.43 % |
20.43 % |
| 3 |
4,396×692 = 3,042,032 |
19.01 % |
19.01 % |
| 4 |
9,056×263 = 2,381,728 |
14.89 % |
14.88 % |
| 5 |
7,686×758 = 5,825,988 |
36.41 % |
36.41 % |
| NO.1~NO.5 小計① 15,998,884 |
100 % |
| |
6 |
2.0625×1.68 = 3.465 |
0.12 % |
0.00 % |
| 7 |
8.51×20.5 = 174.455 |
5.91 % |
0.00 % |
| 8 |
654.5×4.21 = 2,755.445 |
93.30 % |
0.02 % |
| 9 |
0.3748×0.713 = 0.267 |
0.01 % |
0.00 % |
| 10 |
3.328×5.875 = 19.552 |
0.66 % |
0.00 % |
| NO.6~NO.10 小計② 2,953.184 |
100 % |
| (小計①+②) 合計 16,001,837.184 |
|
100 % |
| NO |
11 |
¥5,286×675 = ¥3,568,050 |
% |
% |
| 12 |
¥2,814×856 = ¥2,408,784 |
% |
% |
| 13 |
¥7,529×631 = ¥4,750,799 |
% |
% |
| 14 |
¥38,541×29 = ¥1,117,689 |
% |
% |
| 15 |
¥8,638×795 = ¥6,867,210 |
% |
% |
| NO.11~NO.15 小計③ ¥18,712,532 |
100 % |
| |
16 |
¥8,775×3.32 = ¥29,133 |
% |
% |
| 17 |
¥2,520×0.625 = ¥1,575 |
% |
% |
| 18 |
¥7,562×15.5 = ¥117,211 |
% |
% |
| 19 |
¥712×0.0567 = ¥40 |
% |
% |
| 20 |
¥4,824×1.375 = ¥6,633 |
% |
% |
| NO.16~NO.20 小計④ ¥154,592 |
100 % |
| (小計③+④) 合計 ¥18,867,124 |
|
100 % |
さて、出来ましたでしょうか? 答えは下記の通りです。
【練習問題の解答】
| NO |
11 |
19.07 % |
18.91 % |
| 12 |
12.87 % |
12.77 % |
| 13 |
25.39 % |
25.18 % |
| 14 |
5.97 % |
5.92 % |
| 15 |
36.70 % |
36.40 % |
| |
100 % |
| |
16 |
18.93 % |
0.15 % |
| 17 |
1.02 % |
0.01 % |
| 18 |
75.74 % |
0.62 % |
| 19 |
0.03 % |
0.00 % |
| 20 |
4.29 % |
0.04 % |
| |
100 % |
|
|
100 % |
以上でパーセントの計算に関する説明は終了です。次は計算する順序と採点箇所についてです。
■採点と計算する順序について
ここでは採点と計算する順序について説明します。
まず採点についてですが、乗算の場合は見取算とは違い、全てが採点箇所の対象になるのではなく、ランダムに25箇所設定されています。得点の配分はパーセント以外の無名数と名数の計算を合わせて6割、左側のパーセントが2割、右側のパーセントが2割となっています。
1級~3級は7割以上が合格なのでそのレベルを目指すのであれば、上記で説明した順序(パーセント以外の無名数・名数の計算 → 左側のパーセントの計算 → 右側のパーセントの計算)で計算した方が、時間が間に合わなくても右側のパーセントの計算以外さえ全て出来ていれば、8割に到達できるので無難かもしれないです。
ただ別な方法として、例えばNO.1~NO.5の小計を出して、その時点でM+を押し、即パーセントの計算をするなど色々とあります。どの方法が早いか(良いか)は、自分に合う、合わないというのもあるので、同じ問題を別な方法で計測するなど、色々と試してみると良いと思います。もし、段レベルの実力者が近くにいるのならば、どのような方法で計算しているのか参考程度に聞くのも良いと思います。
以上で乗算については終了です。今回、初めて乗算について触れたという方であれば、内容が濃い分、おそらく大変だったと思います。ただ、ここを理解すれば、第10回で説明する除算もすぐに理解できますので出来るまで復習しましょう☆。次は乗算の練習です。次回も頑張っていきましょう!
[最終更新日:2023年6月8日]
・サイドバーを含め、一部修正しました(2023年6月8日)
・スマートフォンでも見やすいように文字を大きくし、レイアウトも変更しました(2019年8月25日)
・スマートフォンやタブレットでオーバーレイ広告が出ないように仕様を変更しました(2017年10月1日)
・練習問題のNO.14の式に誤りがありましたので訂正いたしました。間違いをご指摘いただいたニックネーム:クリスタベル様に感謝致します^-^(2012年11月20日)
・2007年に公開していた内容をリニューアルしました。(2008年9月13日)
|

