こんにちは。KOです。今回は、複合算についてです。この複合算は電卓のメモリ機能(Mの機能)を使用して計算しますが、メモリ機能については第3回で学習しており、そこで既に桁数の少ない複合算の練習問題も行っています。
おそらく、メモリ機能を理解できていれば、すぐに出来ると思います。もし、忘れてしまった方は「第3回 メモリ機能について」を復習しましょう。従って、ここではメモリ機能の詳しい説明は省略し、複合算の端数処理と練習問題を中心に行っていきます。では、今回も頑張っていきましょう!
| 【今回の講座内容】 |
■複合算の概要
■複合算における端数処理
■練習問題 |
■複合算の概要
まず、複合算とは、下記の例のように、加算(足し算)、減算(引き算)、乗算(掛け算)、除算(割り算)の四則演算が混ざった計算のことをいいます。
【例】(54,677,168÷799)+311×1,697
もし電卓を使わないで計算するのであれば、まず一つ目の式を計算し、その答えを紙に書き、続いて二つ目の式を計算し、また紙に答えを書き・・・のように計算するかと思います。ただ、電卓の場合は紙に書くのではなく、「M」の機能を利用して効率よく計算しなければなりません。
また、全ての計算において端数が出た場合は、問題用紙の上に記載されている(注意)に準じて処理していきます。この端数処理については乗算、除算とは異なるので、注意が必要です(後ほど説明します)。
さて、ここでもしかしたら今の文章を読んで「Mの機能を絶対に使わなければならないの?」「紙に書くのと、電卓のメモリ機能を利用して計算するのはどっちが速いの?」「紙に書いて計算しちゃダメなの?」など疑問に思った方もいるかもしれませんので少し補足します。
これは結論からいうと「M」の機能を使用したほうが慣れてしまえば、圧倒的に速いです。おそらく両手を器用に使い、利き腕でない方で文字を書いたとしてもメモリ機能を使用したほうが速いと思います。
実は私も最初の頃に「紙に書いて計算しても速いんじゃないの?(笑)」と思っていたのですが、紙に書いた数字をもう一度見て計算しなければならない手間と、書き間違え・押し間違えを防ぐ為にかかる一瞬の見直す時間等から、その差を実感しました。3級レベルでは紙に書いてもなんとかなるかもしれないですが、上級を目指すのであれば、必ず「M」の機能を使用して計算するようにしましょう。慣れないうちは「M」の機能が難しく感じるかもしれませんが、逆にこれさえマスターしてしまえば、計算自体は単純なので、乗算、除算よりも楽だと思います。
あと、複合算では、当然ながら、級(レベル)によって桁数が違い、3級が1題10桁以内、2級が1題11桁以内、1級が1題12桁以内でそれぞれ20題出題されます。また、端数処理の方法も2級・3級と1級では若干、異なり、2級・3級では整数未満を切捨てて計算するのに対し、1級では小数第3位未満を切捨てて計算します。な制限時間は10分となっています。
複合算の概要はこれで終わりです。次は複合算の端数処理について説明します。
■複合算における端数処理
端数処理についてですが、乗算・除算では四捨五入で計算しましたが、複合算では切り捨てる処理を行います。では、まず、2級・3級に記載されている(注意)の文言を見てみましょう。
≪2級・3級の場合≫
(注意)
整数未満の端数が出たときは切り捨てること。ただし、端数処理は1題の解答について行うのではなく、1計算ごとに行うこと |
※全経の公式サイトの出題範囲より抜粋
まず、最初の文で、「整数未満の端数が出たとき」とありますが、これは言い換えると小数が出たときのことを意味しています。つまり、小数が出たときは切り捨てるということになり、計算結果が小数になることはありません。
これを電卓で設定すると、ラウンドセレクターは切捨てを意味する「CUT」、小数点セレクターは小数未満を切り捨てて、小数を表示させる必要はないので「0」に設定すればOKです。
では、次の「ただし、端数処理は1題の解答について行うのではなく、1計算ごとに行うこと」についてですが、複合算では、二つの式が組み合わさっているので、それぞれの式で端数が発生することがあります。ここでいう1計算ごとというのは、それら二つの式のことを指しています。つまり、解答欄に書く答えに対して端数処理を行うのではなく、その過程で端数処理を行いながら計算するという意味になります。

※この例では分かりやすいように前方から順に計算しています
では、続いて、1級の場合も見てみましょう、
≪1級の場合≫
1級の場合は、2級・3級の端数処理が理解できていれば、難しいことはありません。「整数未満の端数・・・」の部分が「小数第3位未満・・・」に変わっただけになります。
従って、ラウンドセレクターは切捨てを意味する「CUT」、小数点セレクターは小数第3位未満を切り捨てて、小数第3位まで表示させる必要があるので「3」を設定して計算すればOKです。
[1級レベルでの注意点](2015年5月12日追記)
答えが499,999,999,999以上になる場合、ここで紹介している計算方法だと、一部の電卓においてエラーが起きる事があります。事前にエラーが出る電卓なのか下記の問題でテストしておきましょう。
[エラーチェック用のテスト問題] (500,000,000,000+1)-(1+1)
答えは499,999,999,999が正解ですが、エラーが出る電卓ではEと0が表示されます。原因は不明ですが、パソコンやスマホの電卓では問題ないことから、おそらく電卓の仕様の問題かと思われます。ただ、通常、1級レベルにおいて499,999,999,999以上が答えになる問題は1〜3問程度しかありませんので、もし、該当する電卓だった場合は、その部分の計算を飛ばして、後からスタンダードの方法で計算しなおすのも有りかと思います。なお、練習をこなすと、式をみただけで答えが大きくなりそうなのかは判断できるようになるとは思います。 |
以上のように級(レベル)ごとに説明しましたが、理解できましたでしょうか? 一応、文言の意味を解説する為に、細かく説明しましたが、実際は、複合算の問題に入る直前にラウンドセレクターと小数点セレクターを予め設定し、20題全てその状態で計算するだけなので、複合算の場合は、これとこれを設定するんだなという感じで覚えてしまっても全然OKだと思います♪
さて、次は練習問題です。
■練習問題
いきなりですが、まずは、下記の練習問題に挑戦してみましょう。第3回のメモリ機能と、上記で説明した端数処理の方法が理解できていれば、出来ると思います。
【練習問題A】(制限時間2分30秒)
※端数処理は2級・3級の方法で処理(整数未満切捨て)
[1] (54,677,168÷799)+311×1,697
[2] (811+1,457)×(1289+643)
[3] (4,318,982÷58)÷(1,414,236÷26,543)
[4] 6,335×28.2−479,175÷75
[5] (841,326×196)÷(48.7×79)
出来ましたでしょうか。では、一つ一つ解説していきます。
【[1]の解説】
まず、第3回のメモリ機能についてでも説明しましたが、この講座では複合算を計算する際は、どんなときでも、後ろにある式から先に計算します。従って、311×1,697=527,767を計算し、この結果を「M+」を押し、電卓に記憶させます。次に前方の(54,677,168÷799)=68,432を計算します。
そして、今回の問題では二つの式を結んでいるのが足し算なので、68,432と表示された状態で「+」を押し、先程、記憶した最初の式の答えを呼び出すために「MR」を押します。その結果、68,432+527,767という式が出来上がり、これを計算すると596,199となり、これが正解になります。
【[2]の解説】
まず、後ろの式から計算し、(1,289+643)=1,932の結果を「M+」で記憶させます。次に前方の(811+1,457)=2,268を計算します。
そして、今回の問題では二つの式を結んでいるのが掛け算なので、2,268と表示された状態で「×」を押し、先程記憶させた1,932を「MR」機能を使って呼び起こします。その結果、2,268×1,932という式が出来上がりますね。あとは「=」を押すだけです。正解は4,381,776です。
【[3]の解説】
まず、後ろの式から計算し、(1,414,236÷26,543)=53の結果を「M+」で記憶させます。次に前方の(4,318,982÷58)=74,465を計算します。そして、今回の問題では二つの式を結んでいるのが割り算なので74,465と表示された状態で「÷」を押し、先程記憶させた53を「MR」機能を使って呼び起こします。すると、74,465×53という式が出来上がりますね。あとは「=」を押すだけです。正解は1,405です。
【[4]の解説】
まず、後ろの式から計算し、479,175÷75=6,389の結果を「M+」で記憶させます。次に、前方の6,335×28.2=178,647を計算します。そして、今回の問題では二つの式を結んでいるのが引き算なので、178,647と表示された状態で「−」を押し、先程記憶させた6,389を「MR」機能を使って呼び起こします。すると、178,647−6,389という式が出来上がりますね。あとは「=」を押すだけです。正解は172,258です。
【[5]の解説】
まず、後ろの式から計算し、(48.7×79)=3,847の結果を「M+」で記憶させます。次に、前方の841,326×196=164,899,896を計算します。そして、今回の問題では二つの式を結んでいるのが割り算なので、164,899,896と表示された状態で「÷」を押し、先程記憶させた3,847を「MR」機能を使って呼び起こします。すると、164,899,896÷3,847という式が出来上がりますね。あとは「=」を押すだけです。正解は42,864です。
以上、5題の練習問題を行っていただきましたが、実は、この中に端数処理の問題も含まれていました。それは[5]の問題でしたが、全ての問題で端数処理の設定をして計算している為、気づかなかったと思います。従って、本番でも、どの問題が端数処理といったことは気にする必要はありません。
[1]〜[4]の問題は、二つを結ぶ式を結ぶ部分がそれぞれ「+」「×」「÷」「−」の異なるパターンの問題でしたが、常に後ろの式から計算しているので、特に迷うこともなかったのではないかと思っています。つまり、この流れさえ、身に付けてしまえば、複合算は簡単に感じるようになると思います。
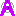 【複合算のPOINT】 【複合算のPOINT】
どんなときでも、後ろから計算し、それを記憶させた後に、前方の式を計算。そして、二つの式を結ぶ部分を計算すること。
では、以上のことを踏まえ、下記の練習問題(3級レベル)にも挑戦してみましょう。
【練習問題B】(制限時間7分30秒) ※解答は一番下にあります。
※端数処理は2級・3級の方法で処理(整数未満切捨て)
[1] (3.581+4.419)+785×3,988
[2] (2,453,061+1,082,625)÷(338.7+123.3)
[3] (8,541−7,519)×26×512
[4] (184.5+62.5)×(48,192−8,936)
[5] (5,781,786÷69)−49,873,289÷68,254
[6] (43,568÷7.1)×(184,921÷765.1)
[7] 3,268×694+1,309,610÷1,514
[8] 7,438×532−812.5×622
[9] (3,300,121−234,240)÷(7,245−6,608)
[10] 38,651,478÷8,377+22,356,052÷41,554
[11] (93,545+221,511)÷(673−285)
[12] (7,481−512)×(4,825−3,986)
[13] (5,707,625÷77)×(987,602÷742)
[14] 2,409,308÷68−116×232
[15] (108,946÷0.048)÷(798×3.1)
さて、制限時間内に15題の問題全て出来ましたでしょうか。これが全て正解出来ていれば、もう複合算で心配することはないと思います♪
以上で複合算については終了です。次回は検定形式の複合算の問題を行っていただきます。頑張っていきましょう!
[最終更新日:2023年6月8日]
・サイドバーを含め、一部修正しました(2023年6月8日)
・スマートフォンでも見やすいように文字を大きくし、レイアウトも変更しました(2019年8月25)
・スマートフォンやタブレットでオーバーレイ広告が出ないように仕様を変更しました(2017年10月1日)
・1級レベルの問題で、一部の電卓にてエラーが起きることが判明しました。それに伴い、1級レベルでの注意点を追記しました。ご指摘いただきましたニックネーム:かお様に感謝いたします(2015年5月12日)
・練習問題Aの解説に一部誤りがありましたので訂正いたしました。間違いをご指摘いただいた「通りすがり様」に感謝いたします^-^(2012年7月26日)
・複合算における端数処理(1級の場合)の一部に誤りがありましたので訂正いたしました。間違いをご指摘いただいたニックネーム:KYO様に感謝致します^-^(2009年4月3日)
・2007年4月22日付けで公開していた内容をリニューアルしました。(2008年9月2日)
【練習問題B】の回答
[1]3,130,580 [2]7,653 [3]13,604,864 [4]9,696,232 [5]83,064
[6]1,478,776 [7]2,268,857 [8]3,451,641 [9]4,813 [10]5,152
[11]812 [12]5,846,991 [13]98,660,375 [14]8,519 [15]917
|

